Once a month I take a more in depth look at a certain type of puzzle. This post I intend to list as many Sudoku variants as possible. There are probably some more around; I welcome your remarks at the bottom of this post. I will not offer a sample puzzle of each variant type. Many of these variants can be found in every SUDOKU magazine. Publishers can develop programs and run that dozens, hundreds or even thousands of times in order to produce puzzles and fill up their magazines. The reason is sheer laziness on my side: Sudoku puzzles are time demanding to produce by hand. I do offer a few exercises where copyright laws allow me to do so, or where I managed to create one myself.
The modern Sudoku started to become mainstream in 1986 by the Japanese puzzle company Nikoli, under the name Sudoku, meaning single number. It first appeared in a US newspaper and then The Times (UK) in 2004, from the efforts of Wayne Gould, who devised a computer program to rapidly produce distinct puzzles. French newspapers featured variations of the puzzles in the 19th century.
A standard Sudoku consists of a 9×9 grid, subdivided into 9 3×3 squares. Every 3×3 square, every row and every column contains each of the numbers 1-9 exactly once. This means a completed Sudoku is also a Latin Square.

The minimum number of clues that is required for a sudoku to have a unique solution is 17, as shown by Gary McGuire∗, Bastian Tugemann†, Gilles Civario‡ in their paper “There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem via Hitting Set Enumeration”, August 31, 2013. Here is a problem with 17 clues:

The puzzle above is presented in their paper as an example of a 17-clue sudoku with a unique solution.
- Sizes: Mini (6*6), normal (9*9) and Hypersize (16*16)
The mini sized sodoku is 6*6 and is often used as a variant for children.
Here is an example of mini sudoku puzzle:
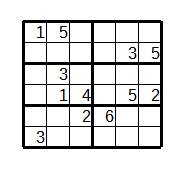
Larger sizes than 9*9 make them more complicated and more laboursome to solve, but the techniques used to solve them are the same as those for a standard size sudoku.You can check your solution here
- Wordoku
As the numbers are just used as symbols, and not for calculation, one may fill the squares with letters as well as with numbers. This comes in esspecially handy if the grid is larger than 3×3.

Some variants, such as in the TV Guide, include a word reading along a main diagonal, row, or column once solved; determining the word in advance can be viewed as a solving aid. A Wordoku might contain words other than the main word. - Sudoloiqs
There is a combination of sudoku and trivia, which I described under the name sudologiqs. - History sudoku
Another form of trivia sudoku are history sudoku’s. A number of years are given by their description, and once you have figured out the rules the normal rules of sudoku apply. Here is a mini example of a history sudoku:

a battle of badr
b invention of the barometer
c alliance between england and castille
d birth of Claudius II, Roman emperor
e establishment of Chalukya Dynasty in India
f battle of Goodwin Sands
Of course it is perfectly possibe to replace the years with other kinds of trivia such as the number of tribes of ancient Israel (if you fancy a biblical theme), or the year in which a certain hocky match was played if you want to do a sports theme.You can check your solution here
- x – sudoku
In an x-sudoku, the numbers 1-9 also appear once on both diagonals. This variant is very common in sudoku magazines. The diagonals are usually shaded as in the picture below.

- Palindrome sudoku
Like a normal sudoku, but some tiles have been marked to contain palindromes. A palindrome is a sequence that reads the same when read backwards. One of the most well known examples is the sentence “Madam, I’m Adam” with which biblical Adam might have introduced himself to Eve if he had spoken English.

- Hypersudoku, also called “NRC Sudoku”, “Windoku”, and “4 Square Sudoku”
A hypersudoku is like a normal sudoku, but in addition there are four areas which also contain the numbers 1-9 once. The areas are usually shaded:

The english language wikipedia hosts the following example:
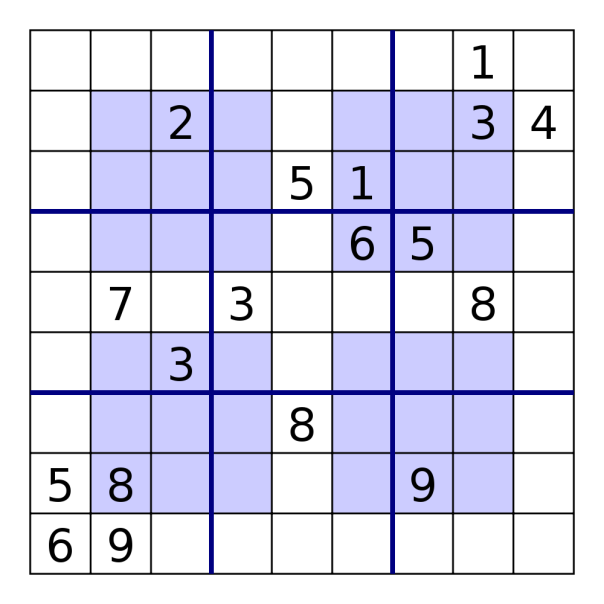
(Presummably by Oceanh, copyright claim CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=2489350)
You can check your solution here
The name NRC derives from a Dutch newspaper. - Odd-even Sudoku
Like a normal Sudoku, but some squares are shaded and may contain only even (or only odd) numbers. This can be made more difficult by shading just som of the odd numbers, not all of them. Or, if even numbers go into the shaded areas, some even numbers, but not all. - Dots sudoku
Like a normal sudoku, but one spot out of every 3×3 square is shaded, and these form an extra 3×3 square. Layout example:

- Trio sudoku or Color sudoku
This variant has al the rules of normal sudoku, but the numbers are divided into three groups. The first group consists of the numbers 1, 2 and 3. They go into the green squares. The numbers 4, 5 and 6 go into the yellow squares. The numbers 7, 8 and 9 go into the white squares.
Here is an example of a Trio sudoku, but with two groups, because it has mini size the 1,2 and 3 are in the shaded spots, the 4, 5 and 6 are in the white squares:

You can check your solution here - Spiralodoku
Like an NRC Sudoku, but the numbers in the extra squares are arranged in a spiral, such as in:

- Chaos sudoku or nonomino or color-sudoku
In Chaos sudoku, the familiar 3×3 squares have been replaced by 9-square areas of different shapes. In the Netherlands, I have seen them published in several magazines.
Here is an example of a chaos sudoku:

(Created by R. A. Nonenmacher, license GFDL, https://commons.wikimedia.org/w/index.php?curid=4787855)
You can check your solution here
- worm-sudoku or chain sudoku or snake sudoku
The numbers 1-9 are used once in every row and column. In addition, there are snakes or worms connected with lines which also consist of the numbers 1-9. There is some variancy in this group, with some of them applying 3×3 grids as well while others don’t. I have seen a copy using circles connected by lines in a publication from Sanders publishing, but I may have seen different forms elsewhere. I feel there is a lot of similarity to chaos sudoku above. - Samurai sudoku’s or Gattai (Japan) consist of 5 overlapping 9×9 grids, as in the figure below. Every 3×3 square contains the digits 1-9, and the ruels for normal sudoku apply to all 5 9*9 grids.

You can find lots of them here.
There are many other shapes into which 9×9 squares can be combined, such as windmills. - Killer sudoku
A Killer Sudoko is a combination of a sudoku and kakuro. The sum of the numbers in each coloured area is given in the upper left corner. - Mirror sudoku or Dependency Sudoku
This variant consists of 2 9×9 squares, which have a different arrangement of numbers, with a small twist: two numbers have been swapped. Suppose the numbers 3 and 5 are swapped. Then every 3 in the left square has a 5 on the same spot in the right square, and every 3 in the right square has a 3 on the same spot in the left square.
This is one of the variants I found at sudoku-variations.com - Diagonal sudoku or Argyle sudoku Sudoku
The name diagonal sudokumight easily be mistaken for X-sudoku. Again, the rules are like normal Sudoku. In addition, some diagonals should contain unique values.

- Greater than sudoku’s or futodukus
Greater than sudoku’s are a combination of futoshiki and sudoku. The English language wikipedia holds a nice example. Be aware, this one is without numbers given as a clue:

(author:de:hd, public domain).
This type of puzzle was first published in Austria (derStandard.at / LeichtSinn) on August 2, 2006.You can check your solution here
- Fortress sudoku
Like normal sudoku, but some squares are shaded to indicate that the value in the shaded cell is greater than the value in the horizontally and vertically adjacent cells. I found the variant at sudokucup - Thermo sudoku
Like normal sudoku, but there is one column (the thermometer) in which the numbers are strictly increasing. Like the previous one, this comes from sudokucup.com - Renban sudoku
In addition to the normal sudoku rules, the diagram holds one or more Renban groups. Each Renban Group is a set of grey painted cells connected to each other, either orthogonally or diagonally. Each Renban Group must hold distinct consecutive digits, in any order. Renban groups may cross across 3X3 boxes / 2X3 boxes / irregular regions. - 3D sudoku’s
3 Dimensional Sudoku’s have been tried in several variants. One of them is Cube Sudoku. The 3×3 squares have been replaced by 4×4 squares, A Cube has 6 surface, which can be viewed as 3 bands of 4 squares each:

You can find more information on them Steve Schaefers page. - Tredoku(TM) is another 3D Sudoku variant. It has many layouts, here is one of them:

- Sojuko
Sojuko’s are a small variant with just one 3×3 block. The sums of the 4 2×2 subsquares are given at the centres.
See Sujoko for more details.
- X-sum
The numbers 1-9 have been placed in a 3 by 3 grid. Sums of the adjacent1,2 or 3 numbers have been entered along the side, as in:

Here is an example of an x-sum puzzle:

This variant can be found too at sudokucup.comYou can check your solution here
- Circle sudoku, also called Round Sudoku, Target Sudoku, Ensaimada or Circular sudoku
In a circle Sudoku, the numbers 1-n (often 1-6, but larger is possible. 1-9 is often used to mimic normal sudoku size) are used once in every “section” and once in every circle disc.

There is a variant in which adjacent numbers are never equal, and differ by at least 2.You can check your solution here
- Sumdoku (1)
There are several forms in which calculations are introduced into sudokus. There are several ways to arrange the digits 1 to 9 into three 3-digit numbers so that one is the sum of the others two. Example: 241+596=837. This can be used to make up one or more of the 3×3 squares, thus diminishing the clues that need to be given.The sums do not need to have a 3×3 size. They may be smaller or larger than 3×3. Arnout Jaspers mentions that a 7×7 example exists in his book “Het labyrint van Occam”. At the end he poses an interesting question: Is it possible to construct a sudoku without any clues, just with lots of additions (or perhaps with other calculations such as products).
You can check your solution here
- Sumdoku (2) or Triploku
In the same book, Arnout Jaspers suggests to add 2 sudoku squares to get a third, like this:

Example: if the upper left corners of X and Y hold 5 and 8 respectively, the upper left corner of Z would be 1, as 5 +16=21. We calculate modulo 10, or simpler said: we look only at the last digit.
He also states that a simple A+B=C additition is not possible.
Fior Triploku, Jasper also introduces a concept that is best translated as “Fully exchangeable”. He means that you can chnage X into Y, Y into Z and Z into X by replacing digits in a certain way, for example by replacing 3 in X by an 8, and so on, and by replacing all numbers in X you get either Y or Z. The same can be applied to Y and Z. - Sumdoku (3) or Arrow sudoku
This variant looks like sumdoku (1), but the scope of the sums is smaller. The summations are usually just one digit, and may be both horizontal and vertical. In Arrow sudoku the dorection of the sum is indicated with arrows. - Tetrodoku or TetrisDoku or Jigsaw sudoku
Part or all of the grid is filled with tetromino’s which are listed besides the main square.

The pieces may be rotated and/or flipped. There is no need to restict one self to L-pieces, as in the example above, or even to restrict one self to tetromino’s. In a way this is a mix of sudoku and a familiar cross-word variation.You can check your solution here
