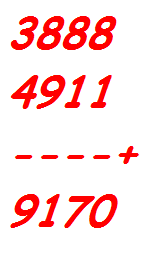Inspector Simon Mart back in London

Back in London, Inspector Simon Mart of Scotland Yard looked at the interrogation reports before him. All three were known criminals, and now suspected of a VST, a Very Serious Theft. In fact, nothing less than the miniature of the royal train carriage had been stolen from the Toy Museum.

It had already been proved that one, and no more than one of them, had stolen the miniature train carriage.

Andy: Billy did it. Charles is innocent.
Billy: Charles did it. Everything Andy says is a lie.
Unfortunately, Charles two statement were in London slang that was totally incomprehensible even to inspector Mart.

1) Billy^*
The officer in charge first wanted to know if Billy could be released – Billy’s lawyer had filed an urgent request that Billy would be allowed to visit his sick mouse in animal hospital.
Suppose Billy is guilty. Then A1 is T, A2 is T. Hence Billy is innocent.

2) Whodunnit?^*
Next of course came the question: Who had done it?

3) The three girls^*
Inspector Simon Mart looked at the next interrogation report. Another VST case, he concluded, and he took a fresh cup of chocolate milk to prepare himself.
Denise, Ellen and Felice had been at the party given by the young Duchess Ginaldino. At the end of the evening, when all three guests had left, it turned out that Ginaldino’s favourite doll, Helen, had been stolen. It was clear that one of the three visitors was the culprit. Young as the three girls were, they were so spoiled that non of them could speak three sentences without lying at least once.

You can check your solution here for no 1 and here for no 2

A new puzzle is published every friday, at which time I will also post the solutions to the previous weeks puzzle so you can check yours. I welcome your solution times, but please don’t publish your solutions – that might spoil the fun for others. I also welcome your remarks on the difficulty level, multiple solutions, ambiguities and so on.

Dissections – the Greek cross

The Greek cross consists of 5 squares joined in the shape of a cross.

1) Greek cross – 4 equal parts^*

The figure above shows a strangely formed meadow between a brook and mountains. There are 4 wells in the area. The farmer died and stipulated in his will that his land would be distrubuted equally among his 4 sons; all 4 lots would have the same area and shape and contain exactly 1 well.

How was the land divided among the 4 sons?

2) The hindu problem

The greek cross as shown in the illustration to the left, is composed of 5 equal sized squares. Cut the cross into five pieces to form a square. There are 2 solutions. According to British puzzle master Henry Dudeney, the problem is over 3000 years old.

3) How many straight cuts?
Henry Dudeney next comes up with the problem:
How many cuts do you need to divide the Greek cross into 4 pieces, so that with these pieces you can form a square?

4) The Red CRoss Lassie
American puzzle master Sam Loyd recounts the following problem:

In the whole realm of puzzledom, and geometry included, there is nothing so fascinating and eminanetly scientific as the series of problems pertaining to the form of the Greek cross and its peculiar relations to the square, parallelograms and other symmmetrical shapes.
As differing from the well known mathematical problem of converting the cross into a square by the fewest possible number of cuts, attention is called to the following pretty feat of chaninging one cross into two.
It appears that one of our wounded boys in blue who was returning home after being nursed back to life by a faithful Red Cross lassie, begged the red cross from her arm as a keepsake; but she, in true sweetheart style, took her scissors and by a few deft clips, cut the red cross into several pieces, which could be fitted together perfectly so as to make two crosses of similar vsize. It is a simple but beautiful trick, and the satisfaction of guessing it will be as great as if you should win a prize.

You can check your solution here for no 1, here for no 2 and here for no 3, and here for no 4

A new puzzle is published every friday. The solution is generally published one week later. I welcome your reactions on these puzzles: are they too easy, too difficult, are there any multiple solutions? How long did you need to solve it?

Cross out

1) Cross out 5×5^**
In the square below, cross out numbers until the sum is 15 in every row and column:

2) Cross out 7×7^**
In the following square, cross out numbers till you the sum is 15 in every row and column:

This type of puzzle was probably invented by Rita Hovestad or Marenke Wiersma, editors of Sanders Brainteaser no 5.

You can check your solution here for no 1 and here for no 2

A new puzzle is published every friday. The solution is generally published one week later. I welcome your reactions on these puzzles: are they too easy, too difficult, are trhere any multiple solutions? How long did you need to solve it?

Mastermind

Some puzzles are derived from games, such as chess problems, draughts problems or bridge problems. It is rare that a game is built around a puzzle. One such a game is Mastermind, invented by by Mordecai Meirowitz, an Israeli postmaster and telecommunications expert.

For those who don’t know it (are there any such persons in the ‘civilised’ world?), here are the rules. The board is four columns white, and one player sets up a secret combination of colours by selecting 4 pegs from a set of pegs in six colours, as shown in the picture.
The second player has to guess this combination. He may put up his own combination, and the first player will respons with one black peg for every peg with a colour in the correct spot and a white peg for every peg with the colour in the wrong spot. Pegs with a colour which are not in the secret combination are not rewarded at all.

1) 4 colours on 3 spots^*

2) 6 colours on 4 spots^**

There are several variations of the game.
The standard form is one codemaker and one codebreaker. Roles alternate to see who can solve the others pattern is as few guesses as possible. Or in the shortest time.
An alternative is to have several code breakers, not able to see each others guesses, and competing for the fewest number of guesses.
Instead of using colours, one may use digits (0-9), or letters. In the latter case, players are limited to existing words.
More Mastermind puzzles are planned in one of the upcoming e-books.

You can check your solution here for no 1 and here for no 2

A new puzzle is published every friday, at which time I will also post the solutions to the previous weeks puzzle so you can check yours. I welcome your solution times, but please don’t publish your solutions – that might spoil the fun for others. I also welcome your remarks on the difficulty level, multiple solutions, ambiguities and so on.

E-book number puzzles

Today I proudly present our first free e-book!

This e-book contains 30 unique number puzzles. The puzzles range from brainteasers to futoshiki puzzles and matchsticks problems. Some puzzle types have been published on this blog, others are new.

You can download this e-book here